Introduction

As I explained before, I am currently trying a sublexical level analysis, by studying tokens. In my previous post, I presented, in details, the steps I took to retrieve and count various n-grams from my sets of tests, as well as what I was able to observe in terms of quantity and diversity. Following this, I am applying the various data I gathered to a concrete example. The goal of this experiment is to test a theory about n-grams, recognition and model training, which is that the model learns, with the ground truths it trained with, to recognize n-grams and not words or lines. To prove that, I use the outputs given after application of the models from my test sets and more precisely, the recognition’s errors, which are extracted in their n-grams form, and I will compare the number of occurrences between correct outputs and erroneous results.

Creation of a table of token error analysis

Presentation of the process

For this study, I reused the sets “War” and “Other” from the dataset I usually exploit and that I presented here. More specifically, I selected again the pages chosen during the comparative analysis, which are:

Letter 607 Page 3 (other)
Letter 607 Page 17 (other)
Letter 678 Page 1 (war)
Letter 722 Page 1 (other)
Letter 844 Page 1 (war)
Letter 948 Page 1 (war)
Letter 1000 Page 3 (war)
Letter 1170 Page 3 (other)
Letter 1358 Page 4 (other)
Letter 1367 Page 1 (war)

After adding the gold transcription of those pages, I applied three models to them: the model that was trained on the pages of the “War” set (MW), the model that was trained on the pages of the “Other” set (MO) and the model that was trained on the large number of pages which constitute the ground truth (MGT). Afterwards, the goal is to retrieve the errors made by the models, which is a task made easier with eScriptorium. Indeed, it gives the possibility to compare transcriptions, to choose a reference (the gold transcription in our case), and then, to see where it is different for the other models. The eight pages are made of about 2400 tokens (punctuation and numbers were removed) and in total, I retrieved 294 tokens incorrectly recognized, all models combined (however, a token can have been incorrectly recognized by more than one model), which represents about 12% of errors for all the models.

Finally, once those errors were retrieved, I modified a script that I had developed for the “Token analysis” experiment, to adapt it to my current experiment and what I wanted to produce. Therefore, my new script is taking as input the lists of errors retrieved from our source of study (four lists, one for each version). For each list, the script produces three new ones (bigrams, trigrams and tetragrams), which gives me twelve lists in the output file. Then, I integrated all those data in a spreadsheet, with one sheet for each n-gram.

The table of token error analysis by n-grams

The table of token error analysis: how does it work ?

General presentation of the table

There are three versions of the table (bigrams, trigrams and tetragrams), but its structure and the colors used are the same, no matter the n-gram studied. The table contains ten columns, with one used as reference and then, the nine others are working as groups of three. The first column is “Correct transcription” and it contains the reference point to compare to when one of the models made a mistake. After, there is the three groups of three columns (one for each model). First, one column (“Model XX”) provides the wrongly recognized token, and the n-gram(s) that do(es) not match its reference counterpart, is colored in green (there can be several for one token). Second, columns two (“Nb occ CT”) and three (“Nb occ MXX”) are retrieving information from the clean lists of tokens, the list being chosen according to the model concerned in the first column: column two is providing the number of occurrences of the reference n-gram (from “Correct transcription”) and column three provides the number of occurrences of the incorrect n-gram. There are some cases where the n-gram (reference or incorrect) does not appear in the list: when it happens, the cell is filled with ø. For example, in the line below, extracted from the table of trigrams (8th row, 1st page, 1st group (model war)), the first trigram is wrong, and when retrieving the number of occurrences, I can see that bar has no occurrences in the ground truth of the model war, while par appears 103 times.

Correct transcription	Model War	Nb occ CT	Nb occ MW
bar, ric, ade, s	par, ric, ade, s	ø	103

Meaning behind the colors added to the table

The tables of n-grams are filled with a lot of information, giving many results at the same time, so it was important to add some color codes for various elements to ease the understanding of the tables, as well as the observations that will come afterwards. Therefore, there are some groups of three cells completely colored (plus the “Correct transcription” cell as well sometimes) to indicate that they will not be part of the general observations of the token error analysis. Firstly, there are cells filled in red: this indicates that the model correctly recognized the token. Second, there are cells filled in blue: this indicates that, even though the token is not correctly recognized, it will not be part of our analysis because the number of characters of the erroneous token is not the same as the reference token. Consequently, it is not possible to do an exact comparison, because, whether it is a character that has been added or deleted, the error will be split in two n-grams, which would not give an accurate comparison with the reference. Those two colored cells are the same along the three tables. Finally, there are one last group of colored cells not to take into consideration, but this time, their number varied from one table to the other. The cells are filled in grey: the token is indeed not correct, but the problem, this time, is in the n-gram concerned by the error. As the division in n-grams is done token by token, and starting from the beginning, it is common that the last n-gram of the token is not the same number of n-gram as the one studied in the table. For example, in the line below, from the table of tetragrams (3rd page, 11th line), the wrong n-gram is ebu, which is a trigram, and as we are in the tetragrams table, it will then not be taken into consideration and highlighted in grey.

Correct transcription	Model War
nouv, eau	nouv, ebu

Moreover, there are also cases where the tokens are only two or three characters, which means that it is too short for the table of trigrams or tetragrams, but it will be treated (for some) in the table of bigrams. For example, in the line below, from the table of trigrams (2nd page, 26th line), as the wrong token is only two characters, it will be in grey here, as well as in the table of tetragrams but not in the table of bigrams.

Correct transcription	Model War
Un	In

Last but not least, there is also a color that has been added to one of the columns’ table and that has to be taken into consideration, because this is one giving a very useful information for our analysis. In the column “Nb occ MXX”, some cells have been colored in green: those cells indicate that the erroneous n-gram has more occurrences in the ground truths of the applied model than the correct n-gram that should have been recognized by the model. In some cases, when the row involves numerous n-grams, the content of those green cells is in black and white. When the number has been colored in white, it means the erroneous n-gram it counted wasn’t more present in the ground truth than the correct n-gram; therefore, only the black numbers in the green cells have to be counted as the more present, except when the number is ø.

The table of token error analysis: what does it say ?

Results by general numbers

The table

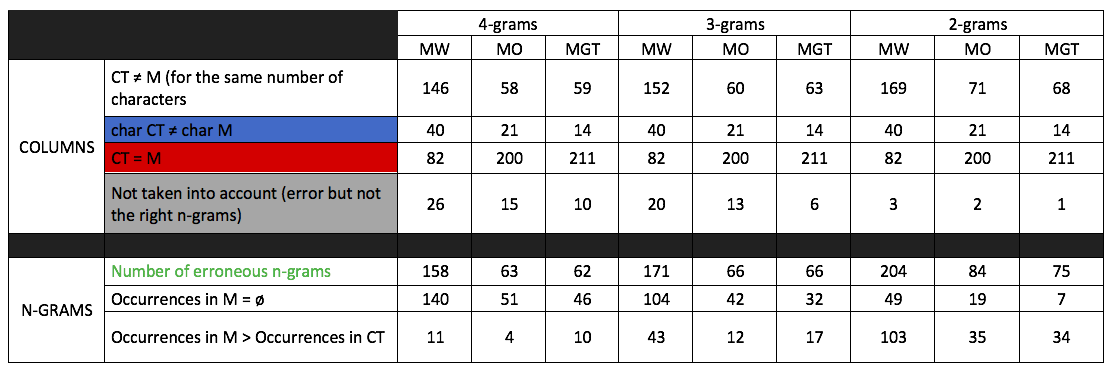
Results from the token error analysis tables (by numbers)

Presentation of the content

This table is divided in two parts horizontally: first, the interest is put in the columns that constitute the table of token error analysis; then, the interest is put in the content of the rows, as in the n-grams that are in it. For those parts, there are also vertical divisions, with three groups of three groups: one group for each type of n-gram (2-, 3- and 4-grams) and then, in it, one column for each model (MW, MO, MGT).
For the “Columns” part, there are four rows, which contain information about the various colored (or not) cells mentioned earlier. Therefore, for each n-gram/model duo, the table provides the number of cells that has the same number of characters in the reference token and in the model applied but not the same output (1rst row), has a different number of characters for the reference token and the model’s output (2nd row, in blue), has the same result in the reference token and the model’s output (3rd row, in red), and are not considered because the error is in an n-gram of a different size that the one it should be in its specific column (4th row, in grey). The total for the four summed rows is always 294, as in the total number of incorrect tokens. The values for the blue and red rows are always the same for each model, from one n-gram to the other, because of the nature of its content.
For the “N-grams” part, there are three rows, which contain information from the group of three mentioned earlier, as in the output of the model applied and the number of occurrences from the token analysis of the applied model. Thus, for each n-gram/model duo, the table provides the number of erroneous n-grams, which is different from the first row because one token can have several erroneous n-grams, the number of cells where the occurrences of the erroneous n-gram is null in the token analysis of the applied model and the number of cells where the occurrences of the erroneous n-gram is higher than the occurrences of the n-gram in the reference token.

Observations

Firstly, for the columns, as I said before, I am not considering in my study everything that has been highlighted in blue, which is the instances where the number of characters of the reference tokens are different from the number of characters from the output of the model output (char CT ≠ char M). The table shows that it does not represent a large portion of the tokens no matter the model, while also being the same from one n-gram to the other: 13% for MW, 7% for MO and 5% for MGT. Therefore, as those numbers are pretty small, I don’t think ignoring them will really impact my results and observations, and it will not make my study too unbalanced.
By observing the numbers in the row “CT = M”, which represents instances where the model produce the same token as the reference, it is possible to observe the large gap between what MW can correctly recognize and what the other two models can do; while MW only has 82 tokens correctly recognized, MO has 200 and MGT has 211, meaning MO and MGT recognized twice more tokens than MW, proving once again that MW is a weaker model, which was already noticed in previous experiments. If we compare MO and MGT, we can observe that, even though the training of MGT was made with way more ground truths than MO, their recognition level seems to be similar here. This can also be observed with the numbers in the row “CT ≠ M”, because they always have numbers that are pretty close: 58 (MO) and 59 (MGT) for tetragrams, 60 (MO) and 63 (MGT) for trigrams, and 71 (MO) and 68 (MGT) for bigrams.
Finally, for the instances where the error was not considered because it is not in the right n-gram, we can observe a decrease the shorter the n-gram gets: there are many that aren’t considered in tetragrams (more than 20 for MW) and still a little for trigrams (20 for MW and 12 for MO). Then, there are almost none left in bigrams (3 (MW), 2 (MO) and 1 (MGT)), which could mean that there are either some one-character token wrongly recognized left or it is tokens with an odd number of characters and the one character wrong at the very end.

With the n-grams, we can gather even more information than with the columns. Foremost, the “Number of erroneous n-grams” row tells us that MW is even worse than what was suggested in the columns, no matter the n-gram in question, but mostly with the bigrams. While there were 146 (tetragrams), 152 (trigrams) and 169 (bigrams) cells that had incorrect outputs, there are actually 158 (tetragrams), 171 (trigrams) and 204 (bigrams) erroneous n-grams, meaning that some tokens have several incorrect n-grams, implying that MW is even weaker than previously thought. Those numbers are also a better indication to separate between the results of MO and MGT, because although MO had sometimes less incorrect tokens than MGT, the erroneous n-grams show numbers equal or bigger than MGT, meaning that MO made more mistakes in the end (trigrams: 60 (MO) and 63 (MGT) but 66 (MO) and 66 (MGT); bigrams: 71 (MO) and 68 (MGT) but 84 (MO) and 75 (MGT)).
Now, if the first line of the “N-GRAMS” part indicated a possible conclusion about the efficacy of the models, the last twos are more an indication about the level of efficacy of the n-grams. For the null occurrences of the erroneous n-gram in the applied model’s token analysis, we can observe a decrease of the number as the n-gram gets shorter, no matter the model (140 –> 104 –> 49 (MW); 51 –> 42 –> 19 (MO); 46 –> 32 –> 7 (MGT)). The numbers are still high with trigrams, but they are considerably less important, compared to the first twos, with the bigrams. It could be concluded that there are more various trigrams and bigrams in the models, even if they don’t have a lot of occurrences. As to the last line of the table (“Occurrences of the model output > Occurrences of the reference”), the results are going the other way around this time, with the number going higher as the n-gram gets shorter, reaching 35 (MO) and 34 (MGT) instances with a higher occurrence of the errors, and an even bigger difference for MW, that has its number multiplied by almost a hundred (11 in tetragrams to 103 in bigrams), suggesting that the errors with MW seem to come from what it learns and mostly in the bigrams. However, although the table says that the occurrences are bigger for the erroneous n-grams, we don’t know the scale of the difference, as it could have 3 more occurrences than the reference n-grams or 30. This will need to be confirmed with an observation of the table.

Results by general percentages

The table

Results from the token error analysis tables (by percentages)

Presentation of the content

Vertically, this table is the same as the previous one, as we have three groups of three groups: one group for each type of n-gram (2-, 3- and 4-grams) and then, in it, one column for each model (MW, MO, MGT).
Horizontally, there are four rows, which give percentage from the quotients obtained with the numbers contained in the table of the previous section. The first two rows use the numbers from the “Columns” part, with a denominator of 294 (as in the total number of incorrect tokens): “Tokens correctly recognized” use the number from the red row as a numerator, and “Tokens with simple substitutions” use the number from the first row (the one with no background color) as a numerator.
The last two rows use the numbers from the “N-grams” columns, and the denominator in both cases is the “Numbers of erroneous n-grams”. “Occurrences where the substitutions ‘makes sense’” use the numbers from the last row, where the occurrences of the erroneous n-gram is higher than the occurrences of the n-gram in the reference token, meaning that the incorrect result could be explained from the results in the token analysis previously done. In the contrary, “Occurrences where the substitution has ‘no base’” use the numbers from the penultimate row, where the occurrences of the erroneous n-gram is null in the token analysis of the applied model, meaning that there is no explanation for this incorrect recognition, as it is not something that it learned in its training.

Observations

From a token point of view, we can see again that there is a consequential difference of recognition between MW and MO/MGT. Only 1/4 of the tokens from the list have been correctly recognized by MW, while it is almost 3/4 for MGT, and slightly less for MO. As for the “simple” substitution (meaning not the blue or grey cells), the percentages are pretty different from one n-gram to the other, or from one model to the other. MW has about half of the tokens that are errors, whether it is in the tetragrams or the trigrams, and almost 3/5 in the bigrams, continuing with what was previously said about being a weaker model. For MO and MGT, the results are pretty similar: there is about 1/5 tokens for the tetragrams, a little more than 1/5 for the trigrams and less than 1/4 for the bigrams. However, even though, the percentages are similar, we can see that MGT has one more point in trigrams but one less point in bigrams. This could mean that MO made more errors than MGT on the “special” tokens, which are the ones not taken into account previously because they did not contain the right size of n-grams.

When we start to look at the percentages of the occurrences, we can firstly see that substitutions start to make more sense as the n-gram gets shorter, which could lead to think that the model learns to recognize the bigrams and not really the trigrams or the tetragrams. MO and MW start with a really low percentage in the tetragrams (about 6%) but it really rises with the trigrams (25 (MW) and 18 (MO)), and it even doubles with the bigrams (50 (MW) and 41 (MO)). This means that, for MW, out of all the substitutions they had in the outputs, only 6% of them made sense regarding the tetragrams extracted from the token analysis, but when it comes to the bigrams, half of them can be “justified”. Even though the progression is not that high, it also goes for MO. As for MGT, the percentages were already pretty good for the tetragrams (about 16%), but this could be explained by the quantity of ground truth in MGT, which was much bigger than those of the other two models. The progression reaches a similar percentage than MW with the trigrams (25%), and for bigrams, its number is between the results of MO and MW (45%). As it was already observed with the other table, we don’t know the scale of the difference between the two columns, and, especially with MGT and its large quantity of ground truth, it would be interesting to see the numbers.
Similarly, the substitutions became less groundless as the n-gram became shorter, going from 74-88% for tetragrams, to 48-63% for trigrams, to 9-24% for bigrams. MW doesn’t have a lot of erroneous tetragrams that rely on results in the token analysis (88% of groundless substitutions) and the number is still more than half for the trigrams (60%), but it decreases considerably for the bigrams (24%). MO follows a quite similar path (80% –> 63% –> 20%). On the other end, MGT already starts way lower than the other two for the tetragrams (74%), it became less than half for the trigrams (48%) and it even decreases to less than 10% for the bigrams. Once again, this could be due to the quantity of ground truth for MGT, which would offer more various n-grams, even if there is only one or two.

General observations

Before focusing on the tables and models individually, I will discuss the results more generally. Firstly, I want to do a little comparison between the general results, especially by comparing the number of cells in red, as in the cases where the model managed to correctly recognized something that one or two of the other models did not, to the number of cells in grey, blue or white in the columns of the other models. For MW, we can see that there are 16 red cells where MO and MGT got it wrong (blue and grey cells included), which represent about 1/5 of all the red cells in MW, and in those 16, there are ten red cells where the errors were studied (meaning no blue cells included). In the opposite, MW has 23 blue cells where the other two models correctly outputted the results, which is about 1/2 of all its blue cells, meaning that half of those mistakes are mistakes made only by this model. For MO, we can see that there are 26 red cells where MW and MGT got it wrong (blue and grey cells included), which represent about 1/8 of all the red cells in MO, and in those 26, there are 18 red cells where the errors were studied (meaning no blue cells included). In the opposite, MO has only five blue cells where the other two models correctly outputted the results, which is a pretty low number comparing to MW but also to all the blue cells (21). For MGT, we can see that there are 25 red cells where MO and MW got it wrong (blue and grey cells included), which represent about 1/10 of all the red cells in MGT, and in those 25, there are 14 red cells where the errors were studied (meaning no blue cells included). In the opposite, MGT has an even lower number of blue cells than MW, with only three blue cells where the other two models correctly outputted the results. Overall, there are also 13 cases where everybody got it wrong (whether it is grey, blue, or white) and among them, there are five cases where the errors were studied (no blue). It is also possible to observe that MW mostly did a good job on its own text, as it is where most of the red cells are located in the table, and the same goes for MO. MGT, which trained with many parts of the dataset, where the content of MO and MW might have been included, had most of its red cells in the MO part of the table, meaning it did pretty well with the text from MO but was less good for the text from MW.

Then, I wanted to focus on the grey parts of the table, which are cells that indicated instances where the model made a mistake, but it is not considered because the error in on an n-gram of the wrong size. I will present the observations from the biggest n-grams to smallest, but it is important to mention before, that there is a recurrence in all three tables: two instances of one-character long token (an “a” that turned into an “s” with MW and an “à” that turned into an “A” with MO”). For the tetragrams, in the total of 51 grey cells, there are 22 cases where it is either three-characters long tokens or ending n-grams of three characters, 25 cases where it is either two-characters long tokens or ending n-grams of two characters, and two cases where the last n-gram is one character long. For the trigrams, in the total of 39 grey cells, there are 19 cases of two-characters long tokens, 12 cases where the last n-gram is two-characters long and six cases where the last n-gram is one-character long. Finally, for the bigrams, in the total of six grey cells and outside the two recurrent cases, the four remaining grey cells are because the error is on the last n-gram which is only one character long (“no, m”, instead of “no, n” or “GE, RL, AC, N”, instead of “GE, RL, AC, H”).

Detailed observations

For each category of n-gram and each model, I tried to answer the three same questions:

When the occurrences in “MXX” are equal to ø, are the occurrences of “CT” also ø ? If not, how many of them has a big number ?
When the cell is green in “MXX” (meaning more occurrences than in “CT”), how big is the difference with the cells of “CT” ?
What is the general range of numbers in “CT” and in “MXX” ?

Table of tetragrams

For the MW group of columns, firstly, there are 140 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as value 67 times, meaning that for about half of the ø “MXX” cells, the model did not know either the correct n-gram or the incorrect one it puts. Moreover, the “CT” column had 10 or fewer occurrences 63 times alongside the 140 ø, meaning that even in the cases where it knew the correct n-gram, it did not see it enough time to learn it. There are only ten cells with a “high” number against those ‘ø’, and except for three (with values of 59, 36 and 21), they barely have more than 20 occurrences.
Secondly, there are 11 instances where the occurrences in “MXX” are bigger than in “CT” (1 5; 1 2; ø 1; ø 9; ø 1; ø 18; ø 2; 1 7; 1 7; 1 18; 7 25). As we can see, the numbers in the “MXX” are barely exceeding 10 or 20 occurrences, but they are still green cells because there are five times when the model did not have the correct n-gram in its ground truth and five times when it only had it one time, which would not have been enough to learn it. There is only one instance where the numbers are a little higher (7 25), where the n-gram are “fran” (CT) and “Fran” (MXX), meaning that it learned to recognize this n-gram more with an uppercase rather than with a lowercase.
Lastly, as for the range of the two columns, the lowest is ø in both cases and the highest is 59 for “CT” and “25” for “MXX”, showing that the numbers in the MW cells do not climb very high.

For the MO group of columns, firstly, there are 51 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as a value 20 times and had 10 or fewer occurrences 20 times, meaning that in majority, the model did not know or barely know either tetragram. There are only 11 instances of “higher” number and just like with MW, there are only very few climbing higher than 20 occurrences, and even then, it is still pretty low (21, 24, 38), except for one cell with an occurrence of 194.
Secondly, there are way fewer instances of green cells with MO, only four (3 11; 17 41; 33 36; 3 8); however, even though the numbers are pretty different with many occurrences this time, the gaps are not very high (+7, +3, +5), except for one (17 41).
Lastly, as for the range of the two columns, once again, the lowest is ø in both cases and the highest is 41 for “MXX”, but 194 for “CT”, with 69 as the second highest and 38 as the third, showing that the n-gram with 194 occurrences is really an exception here.

For the MGT group of columns, firstly, there are 46 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as a value only 13 times and 10 or fewer occurrences only 11 times. In the contrary, there are 22 cells with higher number, which is about half of the “MXX” ø cells, and this time, the numbers are not on the same level as the ones we saw earlier. Among the 22 high numbers, the five highest are 469, 243, 194, 163 and 139, which makes the errors of the model really odd, but those cases would need to be compared with the occurrences for trigrams and bigrams for the same cells, as it would be an interesting way to check if the tetragrams really do have an impact during recognition.
Secondly, there are ten instances where the occurrences in “MXX” are bigger than in “CT” (18 43; 3 6; 5 23; ø 1; 1 4; 4 38; ø 59; 5 97; 7 86; ø 3) and there are a diversity in the results. In some cases, the occurrences are pretty low whether it is “CT” or “MXX” and the gap is not very high (3 6; ø 1; 1 4; ø 3); in others, the occurrences in “MXX” are getting higher, as well as the gap with the occurrences in “CT” (18 43; 5 23; 4 38; ø 59; 5 97; 7 86), two of them even have a gap of 80-90, which could explain the incorrect recognition.
Lastly, as for the range of the two columns, like for the two previous models, the lowest is ø in both cases. The highest is 97 for “MXX”, with 86 and 59 as second and third highest respectively. For “CT”, the highest is 469, with 243 and 194 as second and third highest respectively, which are way bigger numbers than for the two previous models, demonstrating the size difference of their ground truth.

Table of trigrams

For the MW group of columns, firstly, there are 104 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as a value 47 times and 10 or fewer occurrences 49 times, meaning that in majority, the model did not know or barely know either trigram. There are only eight cells with higher number, and except for two cells (38 and 36), the others barely exceed 20 occurrences.
Secondly, there are 43 instances where the occurrences in “MXX” are bigger than in “CT” (1 5; ø 4; ø 7; ø 2; ø 4; ø 19; ø 1; 9 18; 2 140; ø 140; ø 103; 11 103; 48 67; 8 61; 23 61; 2 61; 2 56; ø 41; 10 36; 1 29; 1 29; 8 25; 7 24; ø 18; 1 17; 2 15; ø 14; 9 12; 1 7; 1 7; ø 7; 2 7; 3 6; 1 6; ø 6; 1 6; ø 5; ø 3; ø 2; ø 1; ø 1; ø 1; ø 1). For 28 of them, this can be explained by the fact that the value in the “CT” column is ø or “1”. However, there are also some instances where, even if the cell value in “CT” is at ø, the occurrences in “MXX” are pretty high (2 140; ø 140; ø 103; 11 103; 2 61; 2 56; ø 41), with gaps sometimes of more than a hundred, which could go towards the theory that trigrams might have an impact during the recognition.
Lastly, as for the range of the two columns, the lowest is ø in both cases. The highest is 140 for “MXX”, with 103 and 67 as second and third highest respectively. For “CT”, the highest is 130 with 103 and 80 as second and third highest respectively.

For the MO group of columns, firstly, there are 42 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as a value 11 times and 10 or fewer occurrences 20 times. There are 11 cells with higher number, with one very high number of 246 and then, numbers at 68 or 45, which are not very high occurrences, which could explain why the model still had recognition difficulty.
Secondly, just like for its tetragrams, there are few instances (12) where the occurrences in “MXX” are bigger than in “CT” (2 3; ø 10; 1 11; 4 11; 3 12; ø 17; 4 26; 17 37; 42 43; 9 58; 45 286; 7 45). Except for one specific instance (45 286 –> “gue” “que”), even though the cells were green, the numbers are usually not very high.
Lastly, as for the range of the two columns, the lowest is ø in both cases. The highest is 286 for “MXX”, with 58 and 45 as second and third highest respectively. For “CT”, the highest is 246 with 214 and 96 as second and third highest respectively. This seems to show that except one specific case, the majority of errors by the model don’t come from its ground truth, because those are not forms that it learned much or more than the real n-grams.

For the MGT group of columns, firstly, there are 32 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as a value only five times and 10 or fewer occurrences only five times, too. In the contrary, there are more than 20 cells with higher number, such as 513, 353, 325, 272, 248 or 168. If the number of ø value is lower than with the tetragrams (-14), there are almost the same number of errors “that do not make sense”. However, there seems to be a continuity from one n-gram to the other, because the five highest numbers of occurrences are from the same tokens as in tetragrams.
Secondly, there are 17 instances where the occurrences in “MXX” are bigger than in “CT” (ø 1; ø 1; 1 4; 2 8; 5 10; 9 11; 9 11; 8 26; 2 53; ø 57; ø 59; 4 65; 16 70; 4 86; 138 140; 19 1744; 53 336). Once again, there is a diversity in results, with pretty low occurrences and gaps (ø 1; ø 1; 1 4; 2 8; 5 10; 9 11; 9 11), and with few cases with really high gaps (4 65; 16 70; 4 86; 19 1744; 53 336), with even one difference located in the thousand, which once again could explain the incorrect recognition, as it is likely that it proposes the trigram it met 1700 times in its ground truth, against the one it encountered only 19 times and might not have really learned.
Lastly, as for the range of the two columns, the lowest is ø in both cases. The highest is 1744 for “MXX”, with 395 and 316 as second and third highest respectively. For “CT”, the highest is 1748, with 513 and 353 as second and third highest respectively. Although the numbers reach really high level, we can still observe that there are only two cases in the thousand, which are “que” and “ont”, i.e. some very specific n-grams as they can exist independently as tokens. The next two are ‘only’ in the 500, which is already way less.

Table of bigrams

For the MW group of columns, firstly, there are 49 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as a value 12 times and 10 or fewer occurrences 25 times. There are 12 cells with higher numbers, varying from large numbers (186, 173, 142 and 124) to medium (63, 43, 35, 33 and 23).
Secondly, there are more than 100 instances where the occurrences in “MXX” are bigger than in “CT” and once again, there is a lot of variety: sometimes, the numbers are very low and so are their gaps (ø 2; 1 9; 7 10; 14 19; 24 26), other times, the numbers are higher but on both sides (173 200; 116 134; 107 134), and finally, there are also times when the numbers are climbing, and the gap is widening (58 365; 24 442; 1 239; 7 265, ø 365). Over those 100 instances, about 1/3 of it concerns green cells, with more than 100 occurrences.
Lastly, as for the range of the two columns, the lowest is ø in both cases. The highest is 442 for “MXX”, with 365 and 271 as second and third highest respectively. For “CT”, the highest is 442 with 302 and 241 as second and third highest respectively.

For the MO group of columns, firstly, there are 19 cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had no ø as a value this time but 10 or fewer occurrences 12 times. However, there are seven cells with higher number, three with really high numbers (391, 278 and 105) and the others placed between 10 and 19 occurrences.
Secondly, there are 35 instances where the occurrences in “MXX” are bigger than in “CT” (1 3; 35 68; 49 580; 1 83; 39 68; ø 2; ø 5; 3 10; ø 2; 197 1039; 68 616; 20 532; 113 479; 391 429; 156 364; 28 246; 117 241; 24 193; 9 165; 33 162; 20 134; 20 134; 9 92; 4 75; 62 70; 12 64; 12 64; 61 62; 2 12; 1 8; ø 7; ø 7; ø 6; 2 3; 1 2). There are few cases of low gaps and numbers (about a dozen) but it is mostly high numbers and wide gaps, even sometimes with a difference of 100, 200 or 300.
Lastly, as for the range of the two columns, the lowest is ø in both cases. The highest is 1039 for “MXX”, with 616 and 532 as second and third highest respectively, and with 17 cells of 100 occurrences or more, and 13 of 50–100 occurrences (for a total of 84 occurrences). For “CT”, the highest is 1039, with 616 and 411 as second and third highest respectively, and with 20 cells of 100 occurrences or more, and five of 50–100 occurrences (for a total of 84 occurrences).

For the MGT group of columns, firstly, there are only seven cells in the “MXX” columns that had ø as its value. For those cells, the “CT” column had ø as a value and 10 or fewer occurrences one time each, and five times with different levels of “high” numbers (6569, 3473, 696, 275 and 91).
Secondly, there are 34 instances where the occurrences in “MXX” are bigger than in “CT” (85 1120; 493 2151; 238 960; 199 732; 8 23; 4 75; 35 52; 2 11; 13 174; 1420 2388; 800 3473; 593 1185; 500 2453; 96 223; 63 194; 58 60; 38 142; 35 78; 24 732; 24 202; 21 182; 21 171; 20 44; 20 35; 19 24; 18 463; 18 463; 15 171; 12 500; 10 3473; 10 1034; 8 334; 6 36; 2 7). There are rare cases of low numbers (8 23; 2 11; 2 7), some cases with an almost inexistent gap (20 35; 19 24; 58 60) and then, there are very high numbers with large gaps (10 3473; 8 334; 18 463; 24 732;), even when the opposites are pretty high too (1420 2388; 800 3473; 593 1185; 500 2453), with differences sometimes of more than several thousands.
Lastly, as for the range of the two columns, the lowest is ø in both cases, but there are really only a few cells with only one or two digits in both cases (36 for “CT” and 30 for “MXX”). The highest is 3473 for “MXX”, with 3347 and 2608 as second and third highest respectively, and with six others in the thousands of occurrences. For “CT”, the highest is 6569, with 5894 and 4726 as second and third highest respectively, with 13 others in the thousands of occurrences. Those numbers show that the bigrams, especially with this model, are on a different level as the other, but also that the occurrences exists whether it is of the correct or incorrect n-gram.

Conclusion

For MW, the tetragrams barely have any occurrences, whether it is in “CT” or “MXX” and when there are, the numbers are low. The situation is similar with trigrams in terms of “unjustified” errors, but not with the green cells as there seems to be more “justified” changes with good numbers of occurrences in the “MXX” rather than in “CT”, even though those numbers are still pretty low. Finally, the bigrams still has many ø in “MXX” or “CT”, but the numbers that are on the opposite column are getting higher. Moreover, there are way more occurrences in the green cells with consequent gaps.
For MO, the tetragrams are similar to MW, there are barely any occurrences in the incorrect or correct n-grams and the numbers are really low, except for one single case, which could be explained by the fact that it is a conjunction. There are more occurrences in the “CT” rather than “MXX” with the trigrams, but the numbers are still very low, meaning that the trigrams might not really be considered, as there are barely any “justification” with them and there are not many learned forms. Lastly, for the bigrams, there are way less unknown n-grams and way bigger numbers. When there are errors, it seems to come from big gaps in occurrences with sometimes very high numbers, and we can also observe that almost half of the erroneous n-grams come from “justified” errors.
For MGT, the tetragrams don’t seem to really have any impact, as they have few high numbers, few cases of high numbers against ø in errors and few instances of explained errors. The trigrams have more “unjustified” errors because there are some high numbers, and sometimes in more cases than in cases with ø as value. However, there are also high numbers that “explain” the error in recognition, with also some wide gaps, as the model already seemed to be learning much with trigrams. At last, the bigrams have barely any unknown n-grams, no matter if it is “CT” or “MXX” and there are very high numbers and wide gaps. Similarly to MO, almost half of the erroneous n-grams came from “justified” errors of the models. For the other half, we can observe that whether it is in “CT” or “MXX”, there are usually some pretty high numbers of occurrences and gaps that are not always very wide, even if “CT” has more occurrences. The only odd results with MGT are five instances of “unjustified” errors, even more so by the fact that the occurrences in “CT” were pretty big, whether it is trigrams or bigrams, while it was low or even ø in “MXX”, so those mistakes really seems to have no ground whatsoever.

From those conclusions, we could say that with a small model (MW), the trigrams and bigrams seems to both have an impact on the recognition, as the model could need to rely on different size of forms to output a result, even though it might not always be enough, as the double numbers of errors for MW comparing to MO/MGT can show. Then, with a mid-size model (MO), the bigrams only seems to be considered, as the numbers of occurrences in trigrams and tetragrams might be too low in comparison. Finally, with a big model (MGT), the tetragrams and trigrams might be taken into account, but it is the bigrams that seem to be the most important, as it has a considerably higher number of occurrences. With so many occurrences, the errors might come from a better knowledge of one form over another close to it when in the process of recognition, and when it knows both forms really well, it could also be confusion.