Multilingual model experiment
- Why this experiment?
- The hypothesis
- The dataset
- Token and alphabet analysis
- Comparative analysis
- Token error analysis
- Conclusion
Why this experiment?
My objective here is to extend the experiment on n-grams that I carried out with the d’Estournelles collection, but with a new dataset. I am using here a different collection, from another project I am working on. Moreover, while d’Estournelles was only French documents, I am working here with a multilingual dataset. I want to see if what I have already observed appears here too, and thus if the n-grams have an impact depending on the multilingual aspect in the case where the same n-gram is found from one language to another.
This experiment is intended to also be beneficial to the project from which I retrieved my new dataset. By recovering ground truth and training a model to conduct my experiment, I am also generating a multilingual typescripted recognition model for the people I am working with in the EHRI project, provided that I succeed in developing a high accuracy model.
The hypothesis
My hypothesis with this additional experiment is that if the model works quite well, but it doesn’t seem to be explained at all through n-grams, that is to say we don’t really encounter numbers and situations similar to those found in the Token error analysis experiment, this will complete the previous experiment. It was not completely conclusive, but in addition to this one, it would be possible to admit that indeed n-grams are not really impactful. A reflection might also need to be made in the case where recurring n-grams are found depending on the various languages, but the model is not good at recognition.
As I am working with a multilingual model, I want to be as diverse as possible in the evaluation phase. Therefore, I want to have documents from both the training and the dataset, in different languages, but also, if possible, documents that it has never seen, in a language present in the dataset but also unknown languages, to see how he manages to deal with the issue of multilingualism.
The dataset
The dataset has been made from documents of the EHRI project. To obtain more information about it, see https://flochiff.github.io/phd/dataset/ehri/dataset.html
Token and alphabet analysis
To reproduce my token error analysis with the EHRI dataset, I first need to do a token analysis. However, I am working with a multilingual dataset, so I am also adding an alphabet analysis because even though the languages are in Latin script, they all have some unique diacritics, which could be interesting to explore.
Obtaining data
The method
For this analysis, I needed two different elements:
- The distribution of occurrences of the alphabet in the training data, in total but also by language;
- The distribution of occurrences of the bigrams, trigrams and tetragrams in the training data, in total but mostly by language.
For the first task, I used a simple script that would count the character from each language set that I would submit. Once it was done, I cleaned the data retrieved to remove the occurrences of punctuations and numbers, as I am only interested in learning about the alphabet in this experiment, and then I entered all this data in a single table, combining all the languages and adding 0 in the case where one character from the alphabet in one language was not found in the alphabet of another language.
For the second task, I followed the same method that I had used during the token analysis of d’Estournelles’ dataset. I retrieved bigrams, trigrams and tetragrams from the training data. I centralized them in a general document where all the languages were mixed, but I also retrieved them language by language (which can be found here, in order to create comparison between languages (the various results can be found here). To do that, I retrieved the most and least common n-grams in each language and I used a script similar to the one I had used during the token analysis to retrieve the common n-grams between languages.
The results
- Distribution of the alphabet by characters (Multilingual model EHRI)
- Distribution of the alphabet by language (Multilingual model EHRI)
- General distribution of the alphabet (Multilingual model EHRI)
- Heatmaps of common ngrams (Multilingual model EHRI)
The presentation of the content
General distribution of the alphabet
This table presents the distribution of the alphabet: the rows present the characters (and are classified from the highest number of occurrences to the lowest number) and the columns present the language. Then, in each cell is the number of occurrences of the characters in the language of the column. The last row of the table gives the total of characters for each language, and the last column gives the total of occurrences of the character of the row. Then, this table was transformed into a heatmap to observe the distribution of characters but also some special cases : the coloring was applied to the whole table with no distinction and the redder a cell is, the highest its occurrence number.
Distribution of the alphabet by characters
This table presents the distribution of the alphabet by character, which means that the rows are classified from the highest number of occurrences of a character in all language combined to the lowest number. Then, for each character, there is the distribution of occurrences among the languages. For each column, the number of occurrences of the character has been divided by the total number of occurrences of the character, which was then transformed into a percentage. Finally, this table was transformed into a heatmap, as a way to observe more easily some distribution between language: the redder a cell get, the highest the percentage.
Distribution of the alphabet by language
This table presents the distribution of the alphabet by language, which means that the rows are classified into alphabetical order. Then, for each column, the number of occurrences of the character has been divided by the total number of characters in the language of the column, which was then transformed into percentage. Finally, this table was transformed into a heatmap, but this time, contrary to the previous heatmap, the coloring is not general to the whole table, but it is done by language. This means that, in a column, the redder a cell gets, the more present this character is in the language set.
Heatmaps of common ngrams
Here, there are three tables, one for each size of n-grams (bigrams, trigrams and tetragrams) and each table is divided in two parts: one for the most popular tokens (red) and one for the least popular tokens (green). Those tables are cross tabulation as the rows and columns have the same values, which explain that there are seven black cells in the table, as no comparison can be done with the same language. In those tables, the number in each cell indicate the number of n-grams that the two languages had in common. Then, a heatmap was added for both parts, to observe more easily the cases where many n-grams were in common between two languages.
Observations
Alphabet analysis
It is possible to observe many things from the alphabet heatmaps, the tables completing each other or sometimes bringing context to understand it more easily.
First, in the general distribution of the alphabet (GDA), I see that the first rows are mostly made of common letters across every language, with a pretty consistent distribution. Afterwards, the distribution usually stays consistent, but there are also some irregularity. For example, the “N” is highly ranked in the table, but it is really only found in one language and a half; the “v” has many occurrences in Czech and Hungarian, but it is inexistent in Polish. The “N” seems also to be an exception in the cases of the presence of uppercase characters at the top of the table, because except “N”, “D” and “H”, those uppercases are mostly at the end of the table. At the very bottom, the uppercases letters that are found are characters that are not among the most common in the languages selected, like “X”, “Q” or “Y” and there are at the very end because we found them in low number and usually in only one language. Although the uppercase characters are pretty inconsistent in the table, the true irregularity of this table are the diacritics, which also reveal lots of information in the other alphabet tables. Those diacritics can have high numbers that would be colored in light red (150 occurrences or more) but they are at the end of the table because those occurrences are only present in one language, which also makes their total, hence the ranking.
We can add more information to those observations by looking at the distribution of the alphabet by characters (DAC) or by language (DAL). Those tables allow a better understanding of the distribution of the letters in the dataset. In the DAC, which is ranked just like the GDA, the top of the table really shows, this time, the data amount difference between the datasets, because the Polish and the Slovak have barely any red or extremely light in their columns, except in the cases where they have single language occurrences or for diacritics common to Czech for Slovak. The DAL shows the distribution in languages which allow us to observe that also all the letters at the top were very red in the GDA, when compared to the number of occurrences in the languages, the distribution is not homogeneous; the brightness of red is not the same from one language to another. The “common” letters seem to be more distributed in Czech and Hungarian, and the Polish and Slovak, with their small dataset, seem to have a good distribution too, although most characters gravitate around 3% of appearance when their presence is not very high. From the DAC, we can confirm some of those observations. The Czech seems to have almost every shade of red, which means that it have a pretty diverse alphabet, with also almost all the diacritics in it and some unique too. German, similarly to Czech, has a lot of red, in very variegated colors. English is mostly present at the top of the table, and it tends to disappear as we go down the table, which could be explained by the fact that the end of the table is mostly diacritics, which is not something present in the English alphabet. Hungarian and Danish are similar to English is this case (except for more diacritics). Polish has not many high percentages in the table (very few red cells).
Finally, the diacritics might be the most striking elements in those tables, because they give contradictory information from one table to another. In the DAC, there are many bright red cells, because there are many cases of all occurrences of a character in one single language or in only two languages. For 108 characters, 30 have 100% of the occurrences and 7 have more than 90% of the occurrences, which means that more than 30% of the table is made by characters found mainly in one language. This gives the impression of great importance to those characters, but it is put into perspective by the DAL, because the numbers that we can observe offer a stark contrast: for the character “ż”, a 100% in the previous table became a “0.1723%” in this table and for “Ő”, it became a “0.0132%”, which indicate that they are not very present in their respective dataset.
To conclude this part, I could say that despite the model being trained from a multilingual dataset, there are many similarities between the languages, which could help with the recognition. There are two problems that could really occur. The first one is pretty common, it is the uppercases, since there are not many in the dataset, that could become a difficulty for the recognition. The second one, and probably the most important, is that there are a wide diversity of diacritics present in the alphabet, with a pretty irregular distribution, which could also become an issue during the recognition.
Token analysis
The distribution of numbers is inverted in the table: for the most popular parts, the numbers go from low in tetragrams to high in bigrams and this is switched for the least popular, although the numbers stay really low in the least popular parts. For the most popular parts of the tables, first, we can see that the tetragrams are not really useful, because the numbers are really low and mostly “0”. Once again, the size of the Polish and Slovak datasets became visible, because they have barely any common occurrences with the others languages in tetragrams and trigrams. The numbers climb a little for the bigrams, but it still pretty poor, for the Slovak mostly. English and German always have the highest common number, no matter the size of the n-gram. Czech seems to have an affinity with every language, even more than English and German sometimes, despite having a dataset of smaller size. In this part of the tables, we can also observe that the difference between the minimum and maximum is usually considerable: in the bigrams, English-German has the highest common number with “236” and Polish-Slovak the lowest with “80”; for the trigrams, English-German is the highest with “140” and Hungarian-Slovak the lowest with “4”; and for the tetragrams, English-German has the highest with “16” and several couples have the lowest (Polish-Slovak, German-Polish, Hungarian-Slovak) with “0”. The English-Slovak disparity can really be found in the table because they are often found in the lowest number of common occurrences: “92” for bigrams, “8” for trigrams and “2” for tetragrams. For the least popular parts of the tables, as seen prior, the small size of the Polish and Slovak datasets is very visible. In the opposite way, the large size of the English and German datasets is also visible, because there are not many common least popular n-grams, which could mean that the dataset was too important for them to have many n-grams with few occurrences and then in common with other languages. Just like it was observed with the alphabet, the Czech dataset seems to be the most balanced language, as well as the one that mix with the others more easily. It is the most colored part of the heatmap and has the most common traits with other languages, no matter the n-gram size. The numbers of highest and lowest occurrences are a little different in scope, and the same goes for the languages related to it: in the bigrams, Slovak-Hungarian has the highest common number with “16” and Polish-Czech the lowest with “3”; in the trigrams, the Czech-Hungarian is the highest with “76” and Danish-Slovak the lowest with “30”; and for the tetragrams, Czech-Polish is the highest with “84” and Hungarian-Slovak the lowest with “12”. The Hungarian and Czech datasets are quite present, and similarly to the fact that this part of the table indicated the low state of the Polish and Slovak dataset and the high state of the English and German datasets, this indicated their intermediate state. To conclude this part, I can say that English and Slovak seem to be the languages that are the most at odds with each other, which could be an interesting observation to take into account. The Czech language seems to be the most balanced language of all, and the German and English languages should be okay in terms of recognition because they seem to really be present in the training data, mostly regarding the most popular n-grams, since that will be what is most useful in the future step of the experiment.
Comparative analysis
After working on the token and alphabet analysis, I decided to conduct a comparative analysis to evaluate the accuracy of the EHRI model that was developed from the training data, as well as to prepare the token error analysis that will come afterwards.
Obtaining data
The method
For this comparative analysis, there were two things that were essential:
- A test set composed of texts of various languages;
- A recognition model adapted to those texts.
I already explained in my presentation of the EHRI dataset what I choose for my test set, as well as the reasons for my choices. To give you a reminder here, I selected ten images and five languages, two for each language and I picked languages already present in the training data, as well as unknown languages to it. The idea is to test its accuracy on languages already learned but also on totally new languages.
The recognition model was produced from the training data that were presented in the EHRI dataset, which are also the data used to generate the alphabet and tokens that were observed earlier. From the 252 documents and seven languages present in the dataset, several models were produced: one for each language and one generic and multilingual containing all the data mixed. Those models have been trained in two different ways: Normalization Form Canonical Decomposition (NFD) and Normalization Form Canonical Composition (NFC). Overall, the accuracy was pretty good, no matter the model and the Unicode normalization chosen, with more than 90-95% of accuracy for the majority.
To do my comparative analysis, since my goal was to see the efficiency of a multilingual model, I used the generic one, but the question was to use whether the NFC or NFD, since their recognition accuracies were similar (97.20% and 97.29%). Having applied both to see if any difference showed up, the results clearly pointed towards the NFC model as the better choice, because of its handling of diacritics. To do my comparative analysis, I manually transcribed the texts of the ten documents I chose. With the way my keyboard works, all characters with diacritics were implemented as a single unit and not a separate one (character + diacritic), which is the same way the NFC model treats the diacritic. However, just like its name indicated it, the NFD model decomposes it, and on eScriptorium (the website I used for my transcription), the comparison system would point an error between a word and its prediction, because the NFD model didn’t “wrote” the character with a diacritic in the same way that I did with my transcription. Therefore, to ease my work and not create unnecessary errors, I chose the NFC model for my comparative analysis (and the subsequent token error analysis).
The results and presentation of the content
The results are available in two formats (versus text and metrics) and in two ways (punctuation and no punctuation). The idea is to get as much information as possible, but also see the impact that the punctuation have on the recognition accuracy, which could help us also determine the efficacy of the model with those signs.
Versus text
The results of the versus text (as well as the metrics) were produced by the KaMI app, by checking the “Create versus text” box: Versus text
Metrics
Those metrics contains a column for each page of the test set. There are eleven rows of results. The second table was obtained by checking the “Ignore the punctuation” box:
- The first two rows are there to indicate the Levenshtein distance, which is the minimum number of single-character edits required to change one word into the other. This distance is given in characters and in words.
- The next three give the Word and Character Error Rate, as well as the Word accuracy. The first and the last sum up should reach 100%. Those numbers gave the accuracy of the model on the page concerned, and the percentage of errors, for word first, i.e., compared to the total of words in the text, and for characters then, i.e., compared to the total of characters in the text. It is interesting to have both because seeing a good WER with a bad CER could indicate that the model is good at recognition except for some words where it was completely useless.
- The next four rows counts the results of the prediction of the model, as in the hits (right character predicted), substitutions (a character was replaced by another), insertions (a new character was introduced) and deletions (a character was deleted).
- The last two rows indicate the total of characters in the reference (the correct transcription) and in the prediction (If there were insertions and/or deletions, those numbers are usually different).
Normal
| EN 1 | EN 2 | DA 1 | DA 2 | SK 1 | SK 2 | FR 1 | FR 2 | IT 1 | IT 2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Levenshtein Distance (Char.) | 48 | 10 | 106 | 14 | 11 | 11 | 67 | 94 | 98 | 21 |
| Levenshtein Distance (Words) | 33 | 9 | 73 | 19 | 14 | 13 | 62 | 94 | 75 | 21 |
| WER in % | 9.85 | 2.325 | 39.673 | 8.636 | 10.37 | 6.046 | 13.596 | 20.042 | 20.215 | 11.351 |
| CER in % | 2.51 | 0.421 | 8.811 | 0.893 | 1.199 | 0.812 | 2.433 | 3.196 | 4.224 | 1.76 |
| Wacc in % | 90.149 | 97.674 | 60.326 | 91.363 | 86.629 | 93.953 | 86.403 | 79.957 | 79.784 | 88.648 |
| Hits | 1867 | 2363 | 1107 | 1557 | 906 | 1343 | 2689 | 2850 | 2226 | 1173 |
| Substitutions | 44 | 7 | 86 | 8 | 7 | 7 | 57 | 83 | 77 | 19 |
| Deletions | 1 | 2 | 10 | 2 | 4 | 4 | 7 | 8 | 17 | 1 |
| Insertions | 3 | 1 | 10 | 4 | 0 | 0 | 3 | 3 | 4 | 1 |
| Total char. in reference | 1912 | 2372 | 1203 | 1567 | 917 | 1354 | 2753 | 2941 | 2320 | 1193 |
| Total char. in prediction | 1914 | 2371 | 1203 | 1569 | 913 | 1350 | 2749 | 2936 | 2307 | 1193 |
No punctuation
| EN 1 | EN 2 | DA 1 | DA 2 | SK 1 | SK 2 | FR 1 | FR 2 | IT 1 | IT 2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Levenshtein Distance (Char.) | 39 | 9 | 106 | 11 | 10 | 10 | 62 | 90 | 90 | 18 |
| Levenshtein Distance (Words) | 24 | 9 | 73 | 16 | 11 | 13 | 58 | 90 | 68 | 19 |
| WER in % | 7.185 | 2.362 | 39.673 | 7.339 | 8.208 | 6.103 | 12.803 | 19.313 | 18.428 | 10.439 |
| CER in % | 2.108 | 0.389 | 9.298 | 0.726 | 1.129 | 0.759 | 2.307 | 3.132 | 3.956 | 1.534 |
| Wacc in % | 92.814 | 97.637 | 60.326 | 92.66 | 91.791 | 93.896 | 87.196 | 80.686 | 81.571 | 89.56 |
| Hits | 1814 | 2308 | 1946 | 1509 | 875 | 1307 | 2629 | 2785 | 2190 | 1160 |
| Substitutions | 31 | 3 | 84 | 5 | 6 | 7 | 46 | 61 | 69 | 12 |
| Deletions | 5 | 2 | 10 | 1 | 4 | 3 | 12 | 27 | 16 | 1 |
| Insertions | 3 | 4 | 12 | 5 | 0 | 0 | 4 | 2 | 5 | 5 |
| Total char. in reference | 1850 | 2313 | 1140 | 1515 | 885 | 1317 | 2687 | 2873 | 2275 | 1173 |
| Total char. in prediction | 1848 | 2315 | 1142 | 1519 | 881 | 1314 | 2679 | 2848 | 2264 | 1177 |
Observations
Among all the results, there is one that is pretty striking: the metrics of Danish 1, which are bad, in itself and compared to all the other texts. There is only 60% of accuracy in the recognition, and the punctuation is absolutely not at fault, as the metrics don’t change from one table to the other. The quality of the image could be an element of response for this situation, as it is in pretty bad quality. Even more so, this text is one of the smallest from the test set, which would mean a shorter denominator to calculate the WER and CER, and so a higher percentage. The versus text, shows, moreover, that almost one word every three words is wrongly recognized, and it is not even single errors but multiple mistakes in the word. Most of the errors seem to be complete gibberish, with no logic, whatsoever, to the substitutions.
Except for this Danish image, the rest of the test set with languages from the training data have a pretty good recognition. English and Slovak have both good, and even sometimes excellent, results (90%, 97%, 93%, and an 86% that becomes 91% when the punctuation is not taken into account) and the other Danish is also rather good (91%). While observing the versus text of those documents, I can see that the problem comes mainly from punctuations, uppercases letters and numbers, which the model seems to struggle with, no matter the languages in question. However, it is not really concerning as it is pretty common mistakes when dealing with post-OCR correction.
The punctuation seems to be a major problem in the recognition, as we can observe in many ways: first, we see noticeable differences from table “Normal” and “No punctuation”, because most of the word accuracy percentages gain one to three points, and it is even a jump of five points for SK1 and when removing punctuation from the study, all the images from the test sets with languages from the training data (except the bad Danish) reach a word accuracy rate higher than 90%, and the IT1 even comes pretty close to it with 89.56%. The number of substitutions tends to also drop a lot when we remove the punctuation from the analysis (44 –> 31 (EN1); 57 –> 46 (FR1); 83 –> 61 (FR2)). The versus text shows that those errors in punctuation are pretty diverse because it can be related to hyphens, commas, or apostrophes.
For the two languages that are not part of the training data (the French and the Italian), there are two kinds of result: one where the WER is 11-13% and another where it is 20%. Although it is not an ideal result, it is not terrible considering that this was done by a model that have never seen those languages when it trained. When looking at the versus text, I can see that besides the problem of the punctuations and the numbers, the main issue that the model encountered was the diacritics, which are heavily present in the Italian and French texts, but with signs that it has never seen before because it does not exist in Czech, Danish or else. This is diacritics such as “è”, “á”, “û”, “é” and it is also an issue that was slightly found with SK2, where some diacritics specific to Slovak were not recognized by the model. Usually, those diacritics are either replaced by a random letter, that could look familiar to the one it was supposed to recognize, or in the case of the French texts mostly, it is replaced by other diacritics, more frequent in the languages of the training data such as “ö”, “d’” or “ø”.
To conclude this comparative analysis, I can say that the results of the metrics are rather encouraging. The model seems to be working on the languages of the dataset, whether it was seen it many times or not much. Moreover, it also works pretty well, according to the metrics, on unknown languages of the same script. The real limitation in those cases is diacritics because it seems to not be able to recognize and transcribe correctly a diacritic if it has never seen it at all or even barely (as it was shown with the Slovak set). The model also struggles with numbers, uppercases, and punctuations, but it can be considered a minor issue here. Overall, the results are more auspicious than could be expected, and the model seems to be already available to be put to good use.
Token error analysis
With the comparative analysis conducted, the EHRI model was applied to ten different documents, which expectedly generated errors, which can then be used for the token error analysis.
Obtaining data
The method
For this analysis, I thoroughly retrieved the errors observed during the comparative analysis and I copied them in a spreadsheet. I then did a little cleaning: I deleted cases where the error was on a number, since I am only interested in the sequence of alphabet characters, and cases where two words were jointed due to a missing space, as well as errors in punctuation, as this is outside elements not relevant to the analysis that I want to presently conduct.
Once this was done, I applied on my lists of correct transcriptions and of errors a Python script to create lists of bigrams, trigrams and tetragrams, divided by languages, to help with some analysis of the errors afterwards. The result can be found here. After obtaining my lists of n-grams, I could start my tables of n-grams. To create it, I used the same method as I did for the previous token error analysis, and I retrieved the number of occurrences of the tokens I had in my tables from what I did in my token and alphabet analysis. After filling the tables, I filled in the colors the same way as before. The major difference with the tables from the previous token error analysis is that there is no red anymore in this table. Indeed, previously, one of our observation was to compare one recognition model with another and to highlight when they didn’t make a mistake that another model made. In this case, since I am only evaluating a single model, there is no comparison to be made, so the table is only filled with blue, grey, and green. From those tables, I then extracted general information and information by language, in numbers and in percentage, to create new tables and obtain thorough data on the composition of the tables.
The results
The tables of token error analysis by n-grams
Results by general numbers/percentages

Results by numbers/percentages by language

The presentation of the content
The tables of token error analysis by n-grams
As I explained earlier, the tables are done similarly to the ones from the previous token error analysis. In blue are all the cells that presented errors with a different number of characters than the correct transcription, and in grey are the cells where even though the token might not be correct, the n-gram affected does not have the right number of characters in its sequence. Finally, in green are the cases where the n-gram of the error is more present in the training data than the n-gram of the correct transcription. The only exception in that case come from some white numbers in the green cells: this happened when two or more n-grams are wrong in the row, but not all the n-grams of the errors have more occurrences than the ones in the training data. In those cases, the cells were highlighted in green and the number that should not be taken into account has been written in white.
Results by general numbers/percentages
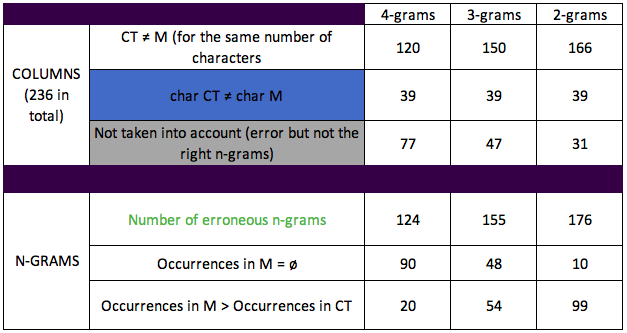
Those tables contain general information from the tables of n-grams. The first one (by numbers) presents results separated by n-grams and is divided in two: columns and n-grams. In the first part of the table, the cells give the distribution for each n-gram of the 236 rows between “Correct transcription is different from the prediction”, “There is a difference, but the number of characters is not the same for the two” and “It is not taken into account because it is not the right n-gram”. The second one is always the same between all three columns, so the first and the last are the ones that change. In the second part of the table, the cells centred on the erroneous n-grams. Firstly, the numbers of erroneous n-grams can be higher than the one in the row “CT ≠ M” because there can be several erroneous n-grams in the same row of the table of n-grams (the token had more than one mistake). Then, I collected the number of cells where there were no record of the erroneous n-gram in the training data of the model and the number of cells where the number of occurrences of the erroneous n-gram in the training data is higher than the correct n-gram. The second one (by percentage) retrieved data collected in the first one and provide percentage for it. In the first row is the percentage of “CT ≠ M” divided by the total number of columns, which signifies what percentage of errors there are if the errors in blue and grey are not taken into account. Then, the next rows give the percentages of cases where the substitution “makes sense” or has “no base”, which means that I divided the numbers in the last two rows of the second part of the previous table with its first row.
Results by numbers/percentages by language
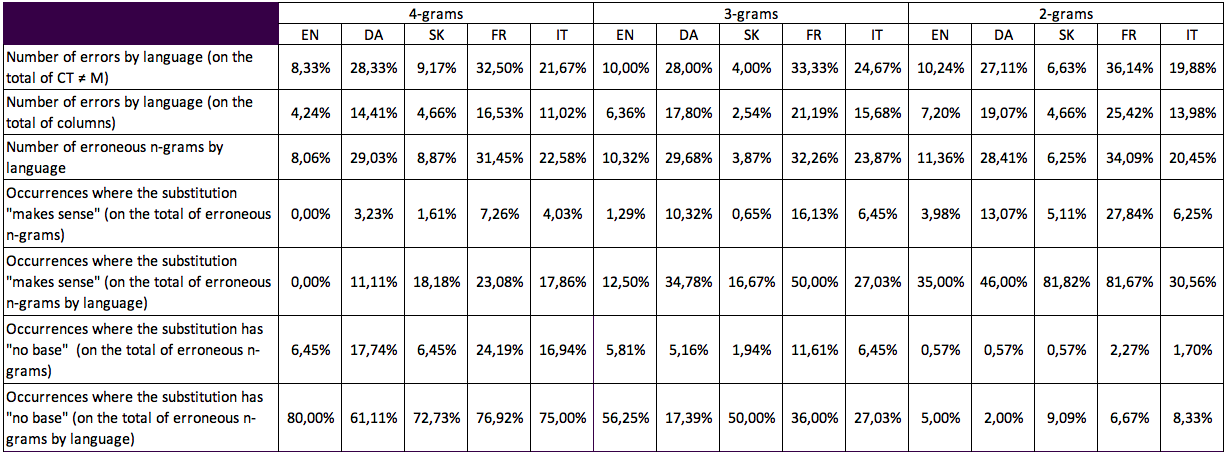
Those tables contain the same information as the previous one but divided into the five languages from the dataset, the idea being, this time, to observe the recognition skills of the multilingual model by language. The first one (by numbers) follow the same principal as the general one, except that each n-gram is separated in five columns, the sum of all giving the number from the general table. The second one (by percentage) contains a little more information than the general table had. This time, I am providing percentage in total but also by language, i.e., the denominator of the divisions to get my percentage is either the number for all languages combined or for the language of the column.
Observations
The tables of results
First, to comment the most general information (i.e. the first two tables), I can see that the errors where the tokens do not have the same number of characters represents 16.5% of each n-gram, which is about 1/6 of the errors. As for the characters not taken into account, they represent 32.6% for the tetragrams, 19.9% for the trigrams and 13.1% for the bigrams. This means that the tokens that are considered in our Token Error Analysis (TEA) represents half of the total for the tetragrams, 63.56% for the trigrams, and 70% for the bigrams. Moreover, by observing the tables more thoroughly, I can see that there are several tokens with more than one erroneous n-grams, even for the tetragrams despite them being large characters sequences: +4 for the tetragrams, +5 for the trigrams, and +10 for the bigrams.
While observing the table of general percentages, it seems, once again, that the tetragrams are ineffective, because there are only 16% of occurrences where the substitution “makes sense” (SMS) while there are 72% of occurrences where the substitution has “no base” (SNB). However, as soon as the size of the n-grams diminishes, the results improve. For the trigrams, there are about 30% for each, but it is really with the bigrams that we see a shift that seems to say that the n-grams are impactful. More than half of the erroneous n-grams predicted (56%) make sense, while only 5% has no base, which is a pretty striking difference from the tetragrams. This seems to lead to the idea that the n-grams might indeed impact the recognition of the model.
To expand those observations, I also wanted to compare the numbers of this general tables to the numbers from the first TEA. I am not comparing the result to all the columns of the previous table, but only to the model Ground Truth (MGT), as it was the more complete model. The training data of MGT is twice the size of that of the multilingual model (MLM), and yet, I can quickly see that the numbers from this percentage table is way better than the ones from the previous TEA. The SMS in tetragrams has the same percentage (16.13%), but it improves a lot for the trigrams and bigrams, by about 10 points (25.76%(MGT)/34.84%(MLM); 45.33%(MGT)/56.25%(MLM)). This phenomenon is also observed for the SNB: despite being half its size, the multilingual model has less SNB (tetragrams: 74.19%(MGT)/72.58%(MLM); trigrams: 48.48%(MGT)/30.97%(MLM); bigrams: 9.33%(MGT)/5.68%(MLM)). The most striking difference, in general, seems to be with the trigrams: I was unsure of its real impact in the previous analysis because the numbers were not always telling but, here, the trigrams seem to be more impactful on the training of the model (+9 points in SMS; -18 points in SNB).
After studying the two first general tables, I am going to get more details on the results with the two subsequent tables, focused on the distribution of languages. First, I am strictly observing the table of numbers. The distribution of the languages confirm what I observed during the comparative analysis: the errors of the model are mostly done in French and Italian, i.e. the unknown languages, and in Danish, because of one image of bad quality. When looking at the number of erroneous n-grams, it seems that it goes up mostly for the Danish, which checked the observation of the comparative analysis: the words are usually completely wrong and not made of single mistakes here and there. Regarding the distribution of null occurrences (“ø”) and higher occurrences in the model than the correct transcription (M > CT), the results are interesting. For the tetragrams, the Danish does not have as many null occurrences as the others compared to the total of errors, which could be explained by the fact that it is one of the training languages. This also happens with the trigrams and bigrams. The numbers decrease as the size of the n-gram diminish, for the languages present in the training data. Those numbers even reach only “1” for those three languages in bigrams, while it stayed pretty high for the models tested in the previous TEA. As for the unknown languages, the numbers are still a bit high (tetragrams: 30(FR)/21(IT); trigrams: 18(FR)/10(IT); bigrams: 4(FR)/3(IT)) but compared to the total of erroneous n-grams, except for the tetragrams, it seems low enough. Finally, no matter the n-gram size, the numbers of “M > CT” appears rather high for French, Italian and Danish, which could indicate that the model indeed choose an n-gram that it learned during its training when in doubt during recognition, especially if it has never seen the language before.
Now, concerning the table of percentages, for the most general part, it appears that, although the Danish has a bad recognition result, it is the French, no matter the n-gram size, that always have the most errors, with, each time, more than a third of the total of “M > CT”. On the contrary, the Slovak produced pretty small percentages, which is impressive considering it was one of the smallest datasets in the training data. Those numbers obviously decrease when compared to the total of columns (the 236 and not just the “M > CT”) but considering, they are still rather high. About the distribution, it is mostly divided between the French, the Italian and the Danish, the English and the Slovak barely accounting for more than 15-18% of the total of erroneous n-grams.
When I concentrate my attention on the occurrences where the substitution “makes sense” (SMS), the percentages do not really rise compared to the total of the erroneous n-grams, specially for the tetragrams. However, as soon as it is compared to the total of errors by language, the percentages become way more revealing. For the tetragrams, the Slovak, and the French have low percentages when compared to the total of erroneous n-grams (1.61% (SK) and 7.26% (FR)), but once it is compared to the total of errors in the language, it reaches almost 1/5 (18.18%) for the Slovak and 1/4 (23.08%) for the French, which already indicates some pretty interesting conclusions that will need to be supported. This remains valid with the trigrams and bigrams, particularly for the French. In trigrams, the SMS represents half of the total of errors in French and in bigrams, it is even more, with 81.67%, which is about 4/5 of the total. The Slovak bigrams present a similar percentage. The Danish percentages are also pretty high: it is not much in tetragrams (only 11.11%) but it represents more than 1/3 of its errors in trigrams (34.78%) and almost half of it in bigrams (46%). The errors in the English appear to be more random, because the percentage of SMS are quite low: none in tetragrams, only 1/8 of its errors in trigrams and a little more than 1/3 in bigrams, while the other languages in this row are higher. The Italian seem to be the strange element here, because the errors do not transpire to come from a bigger presence of the predicted n-grams in the training data. This can be observed with its fairly insignificant percentages and the lack of growth from one size of n-gram to another (tetragrams = 17.86%; trigrams = 27.03%; bigrams = 30.56%): even for the bigrams, which is supposedly the most impactful n-gram, it barely exceeds 1/3 of the total.
When I concentrate my attention on the occurrences where substitution has “no base” (SNB), the percentages indeed diminish when compared to the total of erroneous n-grams, but the percentages of the comparison to the total of erroneous n-grams by language is even more revealing. Compared to the total of erroneous n-grams, we can see that, among the languages, with the tetragrams, the percentage goes from 6% to 24%, with trigrams from 2% to 11% and with bigrams, from 0.5% to 2.2%. Those numbers represent pretty low percentages of SNB, especially compared to what was observed in the previous TEA. However, the difference of percentage is even more striking, when comparing to the errors by language: it goes from 60% to 80% with tetragrams, 17% to 56% with trigrams and 2% to 9% with bigrams. This is a significant reduction, the percentage becoming nine times less important from tetragrams to bigrams. This also tend to support the fact that the tetragrams might not be one of the elements considered by the model when it trains and learns to recognize. Similarly to the SMS, those new percentages are more revealing than the general one, because a simple 6% in total can become an 80% (English tetragrams) and a 1.94% can become a 50% (Slovak trigrams). Those observations comfort me in my idea of adding comparison against the specific numbers of the languages, because the distribution between them is so wide, that it is way more telling to compare it this way, if we really want to learn something about the accuracy of the model and the impact of the n-grams on it. While the Slovak had general percentage that seemed to indicate few SNB, no matter the n-gram size, the percentages of comparison against the Slovak errors, tell a different story: there appear to be many cases where the recognition has no base in tetragrams (72.73%) and trigrams (50%), although it is less the case for the bigrams (9.09%). The Danish has a big diminution in SNB, with 61% of tetragrams, to 17% of trigrams, to 2% of bigrams. Those percentages of the Danish seem to indicate that, no matter the n-gram, the model still had pretty solid ground for the recognition of the Danish, hence the fact that it did not often predict nonsense. The situation with the French errors appears to be similar to that of the Danish: 76% in tetragrams, to 36% in trigrams, to 6% in bigrams. Those percentages tend to indicate that, not considering the tetragrams, the predictions in French are not either complete nonsense, as the numbers are not very high. The result of the English are rather confusing because the tetragrams contain 80% of errors from occurrences of SNB, the trigrams are 56%, which is already way less and only about half of it, and then the bigrams are 5%, which is barely anything in total. This would tend to prove that, if the n-gram have indeed an impact, the bigrams are mostly the one the model is learning from, with some extension to trigrams in some cases. Finally, the Italian percentages did not rise much in the cases of SMS, and it is the same in the cases of SNB: similarly to the other languages, it represents 75% for the tetragrams, but it plunges down to 27.03% in trigrams, to finish at 8.33% in bigrams.
Regarding those various numbers, it would be interesting to see, similarly to the first TEA, the differences of numbers between the occurrences of the correct transcription and the occurrences of the prediction of the model, even when the cell of the prediction column was in green, to verify if the difference is striking. It could be particularly fascinating to do it for the two unknown languages, to see how well better it did. In the cases of SNB, retrieving what the model predicted, but also what are the numbers of occurrences of the correct transcription next to it, could be insightful, to verify if the model had ground to recognize the token in the first place or if it was completely lost by what it had to recognize. Investigating further on the numbers that are neither in one category nor the other would also be a good idea, because for the bigrams, there are more than 60% of the English and the Italian, and 50% for the Danish, for the trigrams, there are more than 45% of the Danish and Italian, and more than 30% for the Slovak and English, and finally for the tetragrams, there are more than 20% of the English and Danish. Therefore, although those numbers seem to show that the n-grams might be impactful to the recognition indeed, which is especially seen for languages not part of the training data, it would be good to support this with observations of the tables of n-grams.
The tables of n-grams
Observations about the distribution of unknown occurrences in the tables
| 4grams | 3grams | 2grams | |
|---|---|---|---|
| Occurrences in CT = ø | 58 | 52 | 35 |
| Occurrences in M = ø | 90 | 48 | 10 |
| Occurrences in CT and in M = ø | 45 | 23 | 2 |
| EN | DA | SK | FR | IT | |
|---|---|---|---|---|---|
| Occurrences in CT = ø (4grams) | 4 | 4 | 0 | 35 | 15 |
| Occurrences in M = ø (4grams) | 8 | 22 | 8 | 30 | 21 |
| Occurrences in CT and in M = ø (4grams) | 4 | 3 | 0 | 26 | 12 |
| Occurrences in CT = ø (3grams) | 4 | 4 | 0 | 36 | 8 |
| Occurrences in M = ø (3grams) | 9 | 8 | 3 | 18 | 10 |
| Occurrences in CT and in M = ø (3grams) | 3 | 2 | 0 | 13 | 5 |
| Occurrences in CT = ø (2grams) | 2 | 0 | 0 | 32 | 1 |
| Occurrences in M = ø (2grams) | 1 | 1 | 1 | 4 | 3 |
| Occurrences in CT and in M = ø (2grams) | 0 | 0 | 0 | 2 | 0 |
In the first table (the general one), I see that, for the tetragrams, there are more unknown occurrences in the prediction of the model than in the correct transcription, and there are also many in both: The double null occurrences are half of that of the prediction and almost all the correct transcription. For the trigrams, there are more unknown occurrences in the correct transcription than in the prediction, although it is not by a big difference; almost half of both the prediction and the correct transcription is a case of double null occurrences. For the bigrams, there are way more unknown in the correct transcription than in the prediction but, this time, there are barely any double null occurrences.
With the second table (the languages specific one), I obtain many more information. First, no matter the n-gram size, the majority of unknown occurrences in the correct transcription are found with the French language, while those numbers are not really high in the prediction. This tends to indicate that the French language is very far from the languages of the training data in any way possible, which could be mostly due to its diacritics. However, this it not the case for the Italian language, because although it might have a high number of unknown occurrences in the tetragrams of the correct transcription, the numbers plunge down in the trigrams and the bigrams. The results of this table can raise some questions about the Slovak: all the content of the test set is known by the model, as there are no null occurrences there, but there are some in the prediction, although not that many, meaning that it was supposed to know what it was transcribing and yet it got it wrong, even more so with character sequences it did not learn in its training. I can observe a similar situation for the English: while it does have some unknown occurrences in the correct transcription, there are not many, and the same goes in the prediction. Finally, the Danish has very few unknown occurrences in the correct transcription, no matter the n-gram size, and although its number of unknown occurrences in the prediction is rather high, it quickly plunges down with the smaller n-grams.
Observations about the content of the tables
In this part, I will retrieve various information from the content of the tables of n-grams. I will mostly try to answer some of the questions that were already in play during the previous Token Error Analysis, which are:
- When the occurrences in the prediction are equal to ø, are the occurrences in the correct transcription also ø (which will pick up some information observed above)? If not, how many of them has a big number?
- When the cell is green in the prediction (meaning more occurrences than in CT), how big is the difference with the cells of the correct transcription ? And, in the other way around, how is the gap between the two?
- What is the general range of numbers in the correct transcription and in the prediction?
I will present my observations, language by language.
The English language in the tables
First, for the tetragrams, there are ten errors that are considered, in the correct transcription, four of them are occurrences unknown to the ground truth and the same goes for their prediction counterpart. In the prediction, in addition to those four, there are also four occurrences unknown from the ground truth. The numbers in the prediction column are quite low, while the ones in the correct transcription can sometimes climb high (149, 122).
Then, for the trigrams, there are sixteen errors considered, four of them in the correct transcription are occurrences unknown to the ground truth and three of those have a null occurrences counterpart in the prediction. In the prediction, ten of the errors are unknown occurrences. The only two green cells of the prediction column do not contain big numbers (37 and 1), while, in the correct transcription column, several occurrences numbers are pretty high (164, 365, 602) and they are usually opposed to some weak n-grams.
Finally, for the bigrams, there are twenty errors considered, and only two are unknown occurrences in the correct transcription, with one unknown counterpart in the prediction, the only one in this column. This time, the numbers in the green cells climb way higher (916, 1087, 1215, 2130), but such is also the case for the correct transcription column (428, 970, 1220, 1697, 1915), and those are opposed, like before, to weak n-grams.
The errors in the English language seems to be a bit about uppercases and when it is not, it usually looks random and no examination of the content of the ground truth and the n-grams seem to be able to give a proper explanation.
The Danish language in the tables
First, for the tetragrams, there are thirty-six errors considered, with four in the correct transcription not known in the ground truth and three prediction counterparts with the same value. In the prediction, twenty-two predictions are unknown occurrences in the ground truth. For this language, the numbers are very low in the prediction and, except in one single case (156), it does not climb much higher in the correct transcription. As for the two green cells in the prediction, it was not really a crushing victory (15/12 and 17/2).
Then, for the trigrams, there are forty-six errors, with four in the correct transcription not known in the ground truth and two prediction counterparts with the same value. In the prediction, eight n-grams are unknown occurrences in the ground truth. Here, the numbers are slightly rising, in both columns. Except in some exceptional cases, the gaps between the green cell of the prediction and its correct transcription equivalent are not that wide (50/159, 13/25, 23/64, 90/240, 93/100). However, in the other way around, there are sometimes significant gaps between the correct transcription and prediction (759/175, 165/21, 243/1). In the prediction, the numbers varied much, but there are a few that are between only one to five occurrences.
Finally, for the bigrams, there are fifty errors considered but this time, none are unknown in the correct transcription. In the contrary, one n-gram is unknown in the prediction, but its correction transcription equivalent is only a 2. There are pretty big numbers in both columns, but the green cells of the prediction usually win by a landslide (134/1215, 91/300, 57/3349, 489/935, 817/1604, 133/1744). There are also some wide gaps the other way around, but it is rather insignificant comparing.
The errors in the Danish language seems to be mostly due to the substitution of similar looking characters such as “s/e”, “s/a”, “m/n”, as well as some uppercases issues. In many instances, and notably for the bigrams, the model, when faced to something unrecognizable to it, for example a character similar looking to another one, seems to have predicted character sequences that it had seen more and was more familiar with.
The Slovak language in the tables
First, for the tetragrams, there are eleven errors considered and none are unknown to the ground truth in the correct transcription. However, except for one cell with an occurrence of “50”, all the other ones only have one to five occurrences. In the prediction, there are only three n-grams that are non-zero, but their numbers are not very high (7, 13, 2).
Then, for the trigrams, there are six errors (as five are not taken into account anymore) and once again, none are unknown to the ground truth in the correct transcription. In this column, the numbers are again rather low, except for one single instance (a 291 matched against an 18). In the prediction, there are three n-grams that have unknown occurrences in the ground truth and the remaining numbers are not very high: the only green cell here is a “3”, matched against a “1” in the correct transcription.
Finally, for the bigrams, there are eleven errors considered again and still no unknown in the correct transcription. In the prediction, there is one unknown n-gram to the ground truth (against a 25 in the correct transcription). The numbers in the correct transcription are still pretty low: three to nine occurrences, 19 to 25 occurrences, and one case of 43 occurrences. One exception to that, an n-gram with an occurrence number of “2274”. In the prediction, the green cells were usually the bigger number by a landslide (260, 279, 157, 418) and the only two ‘losing’ cases are due to null occurrences and a pretty big number (976), unfortunately matched against the “2274”.
The errors in the Slovak language were pretty rare and when they happen, they seem to be mostly happening to the diacritics. The model appears to have predicted diacritics that it knows, rather than the ones that it may have learned during its training, but in such small quantity that it was not enough for it. Therefore, in some of those cases, the Slovak diacritics have been replaced by either the Danish ones or the letter without its sign.
The French language in the tables
First, for the tetragrams, there are thirty-nine errors considered, with thirty-five in the correct transcription not known in the ground truth and twenty-six prediction counterparts with the same value. In the prediction, thirty predictions are unknown occurrences in the ground truth. The green cells of the prediction are not really high and except for two instances (44/60 and 10/64), the victory was against a null occurrence. In the correct transcription, there are only four cases where the occurrences are not null (1, 4, 1 and 18) and their prediction counterparts are always a null occurrence.
Then, for the trigrams, there are fifty errors, with thirty-six in the correct transcription not known in the ground truth and thirteen prediction counterparts with the same value. In the prediction, eighteen n-grams are unknown occurrences in the ground truth and few of them have non-zero counterpart. In the prediction, only two of the green cells do not have a non-zero counterpart (14/25 and 2/11). The numbers in the prediction do not rise above 50, except in about five instances, and, in the correct transcription, except for two cells (71 and 66), the numbers that prevented a ‘win’ for the prediction do not rise above 16.
Finally, for the bigrams, there are sixty errors considered, with thirty-two in the correct transcription not known in the ground truth and only two prediction counterparts with the same value. In the prediction, four n-grams are unknown occurrences in the ground truth and the two with no null occurrences are against an “11” (Q became O) and “8” (l became 1). There are many high numbers in the prediction (30 above 200, 14 above 500, 10 above 1000) and, although, there are some in the correct transcription too, it is way rarer, and it does not go as high as those in the prediction. For the instances where the numbers in the correct transcription prevented a ‘win’ of the prediction, the numbers, except for the null occurrences, were such: 421/123, 709/369, 489/75, 510/49, 44/13, 1664/625, 1101/87. For some of those cases, the facsimile had overlapping characters, which could have prompted the confusion of the model, even though it has known the content, as seen with the numbers in the correct transcription.
The errors in the French language are, in the majority, due to the French diacritics, since many of those are completely unknown to the model. Considering that, it seems to have replaced them by diacritics that it learned to recognize and predict, mainly Czech and Danish diacritics or by the letter without its sign. The bigrams appear to be the mostly impactful here, but the trigrams also seem to have an impact. In other cases, the model did not manage to recognize letters that it had not seen much during its training, like the “q”, so the sequence of characters including that letter is replaced by sequences it knows more.
The Italian language in the tables
First, for the tetragrams, there are twenty-six errors considered, with fifteen in the correct transcription not known in the ground truth and twelve prediction counterparts with the same value. In the prediction, twenty-one predictions are unknown occurrences in the ground truth. There are some exceptional cases of numbers climbing high in the correct transcription (44, 62, 37, 72), but, otherwise, it does not go higher than 10. In the prediction, except for two instances (64 and 60), the green cells do not have numbers higher than 20.
Then, for the trigrams, there are thirty-seven errors, with eight in the correct transcription not known in the ground truth and five prediction counterparts with the same value. In the prediction, ten n-grams are unknown occurrences in the ground truth. There are few cases of high numbers in either the correct transcription or the prediction (9 over 50 and 3 over 100 in the correct transcription; 8 over 50 and 4 over 100 in the prediction). The gaps between the green cells of the prediction and the cells of the correct transcription are rather wide, but the same goes for the other way around, as the correct transcription has high numbers and large gaps sometimes. There are only a few instances where the prediction cells did not become a green cell over barely anything (23/22, 21/15, 155/143, 3/1, 5/2).
Finally, for the bigrams, there are thirty-six errors considered, with only one in the correct transcription not known in the ground truth, its prediction counterpart being a “2264”. In the prediction, three n-grams are unknown occurrences in the ground truth, and they are against an “8”, an “11” and a “196”. There are many high numbers in the prediction (19 above 200, 14 above 500 and 8 above 1000) and in the correct transcription (22 above 200, 14 above 500 and 10 above 1000). Those correct transcription numbers still lost because they were matched against even bigger ones in the prediction (1286/2274, 458/1797, 260/512, 416/1351, 877/1087), although the opposite is also true (1017/516, 258/200, 719/458, 1215/817, 1254/1055, 869/598, 1120/963).
The errors in the Italian language appear to be less linked to diacritics, as it transpired in the comparative analysis. Those results seem to be more baffling, because the numbers are quite high in the correct transcription too, at least for the bigrams. However, in few cases, where the numbers were pretty high in both the correct transcription and the prediction in the bigrams but with a winning margin for the correct transcription, or when it could not be studied with bigrams because it was in the last part of the token (not taken into account), the ‘win’ was for the prediction when looking at the trigrams, which indicate that the trigrams could indeed be impactful in the recognition, especially when the language is unknown. In other cases, the numbers are high in both columns and, as we saw in the previous Token Error Analysis with the model Ground Truth, sometimes when the model knows the n-gram of the correct transcription really well, but knows as well the similar-looking one it puts in the prediction, it can become a source of confusion for the model. Lastly, for some cases where there were overlapping of characters, the model was either too confused to do a right guess and instead predicted gibberish or proposed something close to what it had learned, which happened a few times with uppercases badly recognized or similar looking characters, hence the bad transcription.
Conclusion
Those various languages have different kind of errors and explanation behind it. The conclusion I draw from the last experiment appears to still be standing, and this experiment supports it. The bigrams, as well as the trigrams occasionally, seem to have a real impact on the model. It seems to be a determining element on the training and the recognition skills of the model, as the conduct of this experiment has proven it, notably when the model has barely seen the languages of the text images it is used on or if it has never even seen it at all. This is mostly proven with languages containing many diacritics (as it was for the French here) and the predictions done by the model.
To continue with those observations, I think it could be an interesting move to verify if what was proven here is as effective when the texts are handwritten, and not typescripted like here, especially when the tokens are partly or completely made of characters linked with one another: in those cases, how much do the n-grams play into the model recognition skills.